在风电机组关键零部件的设计中，不仅要考虑极端载荷的影响，还要考虑到疲劳载荷的影响。这是因为在一些风电机组关键零部件，如叶片，轴承座等十几年的使用寿命中，疲劳损伤是不可忽略的一个重要因素。从这一工程实际背景出发，提出了一种适用于时变疲劳载荷的抗疲劳结构设计方法。主要的创新点在于提出了一种新的累计损伤惩罚损伤模型。首先通过准静态有限元分析求得结构位移，再分析计算出所有单元中心处的累计损伤。针对累计损伤在有限元计算的高度非线性问题，本文提出了累计惩罚损伤模型，通过此模型有效地提高了疲劳损伤约束拓扑优化求解的稳定性。此外，由于疲劳损伤是局部现象，因此需要对整个设计域内所有单元的累计损伤进行约束。这会引入大量的约束方程，严重影响求解的效率。因此采用p-norm包络函数对所有累计惩罚损伤约束方程进行凝聚化处理，缩减为单一的约束方程，从而极大程度的降低了计算量，有效的提高了求解效率。若干二维数值算例讨论了不同损伤惩罚参数、平均应力、比例和非比例荷载对最终设计的影响，从而验证了所提方法的正确性和高效性。最后通过三维算例的分析，验证了该方法应用于风电机组关键零部件抗疲劳设计的可能性。以下采用文中的三维算例进行说明：

算例的几何尺寸、设计域、边界条件和载荷条件如图1所示：设计域尺寸为800mm×400mm×100mm，设计域被离散为32000个立方体单元。其中左端面全约束，右端面在如图所示位置受到均布在27个相邻节点的垂直时变载荷F(t)，时变载荷的数据详见图2。时变载荷的循环次数为1×1010次，包络参数μ=""""""4，其余参数与算例1保持一致。本算例讨论了不同疲劳惩罚因子δ（="0.5，1.0和1.5）对结果的影响。优化后的拓扑结果和损伤分布如图3所示。

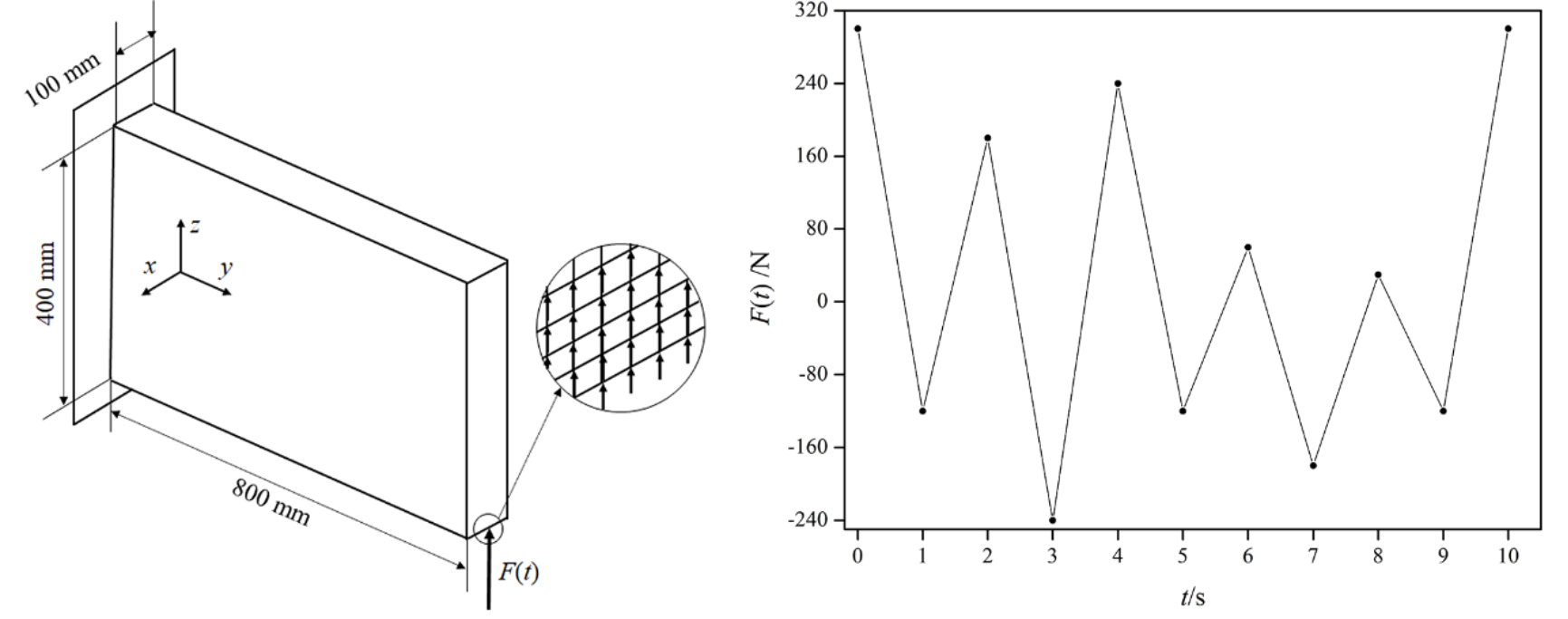
图1. 算例的设计域、边界和载荷条件；图2. 时变载荷谱

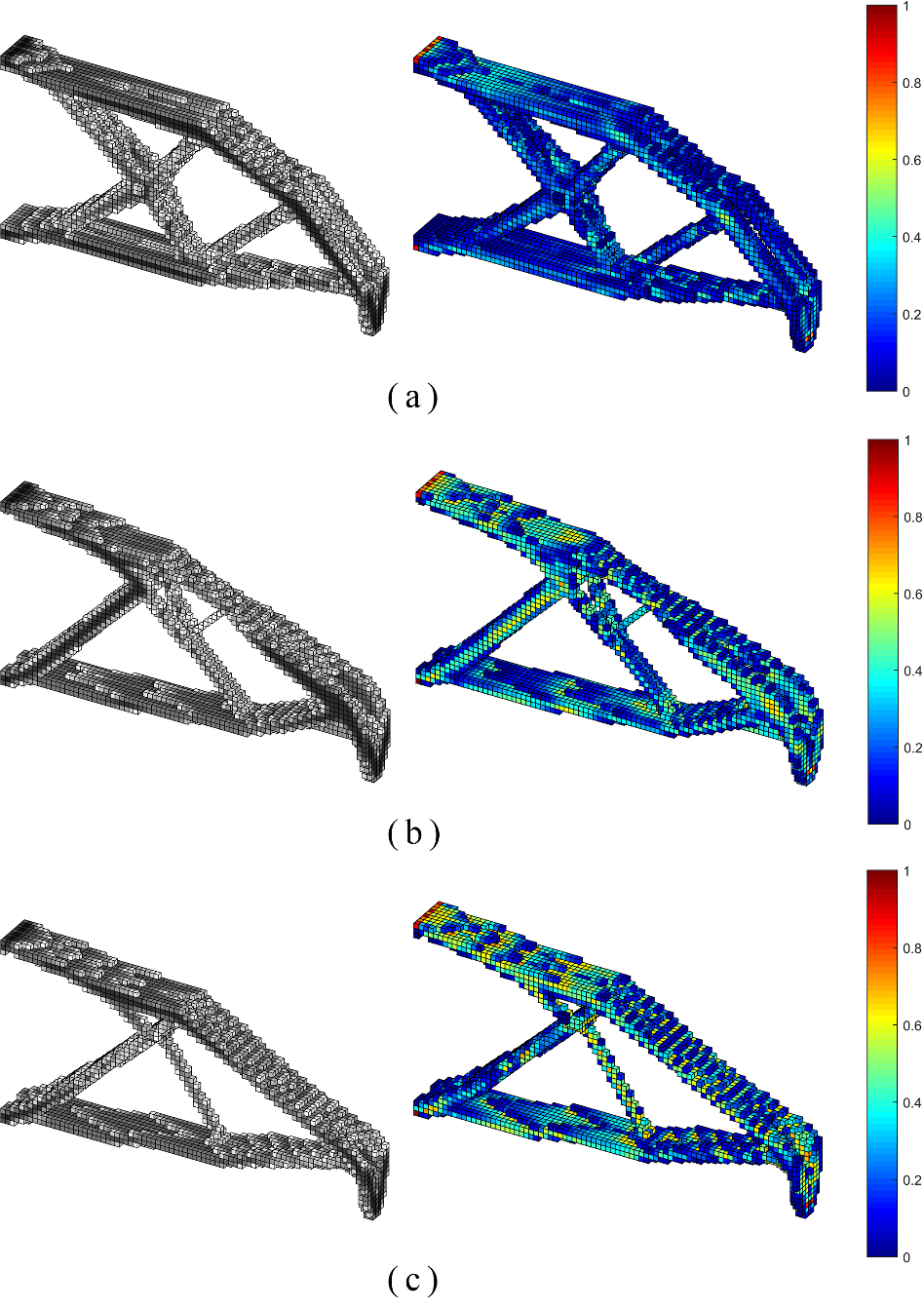
图3. 不同损伤惩罚因子δ下的拓扑优化结果和损伤分布

2020年9月18日，该研究成果以“Fatigue-resistance topology optimization of continuum structure by penalizing the cumulative fatigue damage”为题发表在国际化学领域权威期刊《Advances in Engineering Software》上。该论文第一作者为华北电力大学新能源学院硕士研究生陈卓，通讯作者是华北电力大学新能源电力系统国家重点实验室龙凯副教授，华北电力大学新能源电力系统国家重点实验室是论文唯一通讯单位。

该研究工作得到了北京市自然科学基金、国家自然科学基金和中央高校基础研究基金等项目的资助，论文的发表得到了武汉理工大学文聘副教授的支持。

龙凯课题组在非凝聚方式下的多孔结构优化设计方法取得重要进展

2021年9月30日，国际著名期刊《Materials》在线发表了华北电力大学新能源电力系统国家重点实验室龙凯课题组的最新研究成果“An Aggregation‐Free Local Volume Fraction Formulation forTopological Design of Porous Structure”，提出了一种多孔结构拓扑设计方法。

随着风力发电机组单机容量的增大，风电叶片的尺寸越来越长，因此风电叶片的轻量化设计显得尤为重要。在现代风力发电技术几十年的发展过程中，研究者们提出了很多种在保证风电叶片的结构刚强度满足设计要求的同时尽可能的降低其重量的方法。而放眼于大自然，我们会惊奇的发现鸟类的翅膀不仅能够使鸟类轻松飞行，而且其重量很轻。经研究发现，鸟类翅膀的骨头是一种既具有优异的力学性能，又具有较低的密度的多孔结构。在过去的几十年里，增材制造领域的巨大进步，促进了这种骨状结构的普及。从自然界的这一现象出发，提出了一种新型的多孔结构拓扑设计方法。传统的多孔结构拓扑优化设计方法，比如p-mean包络函数法和隐式约束法在求解的过程中很难满足局部体积比约束。针对这一问题，本文利用增广拉格朗日方法建立一系列最小化子问题，将具有局部体积约束有界的优化问题转化为无约束规划问题，并采用MMA算法进行求解。通过几个数值实验验证了该方法的有效性，进而研究了整体和局部体积百分比、过滤半径和网格规模对最终设计的影响。与现有方法相比，该方法能够准确地限制整体和局部体积分数的最大值，为风电叶片的结构设计开辟了一种全新的可能性。以下采用文中最后一个算例进行说明：

通过对二维骨骼结构进行优化，以验证该方法处理不规则形状和网格的可行性。有限元模型由35,516个单元和35,912个节点组成，其中最外4层单元为被动单元。设计域的底部边缘完全固定，其左上角和右上角在θ=""""""45°方向上受到载荷，如图4所示。两处载荷的大小分别为2545和1697。体积分数的上限分别为φ="0.7，ψ="0.6。为了比较，还进行了不考虑局部体积分数的拓扑优化。图5中显示了两个结果的拓扑结构。

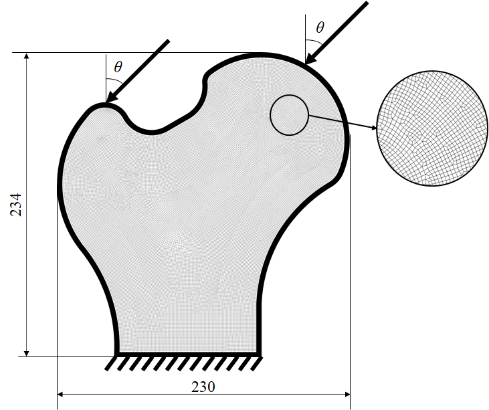
图4. 算例的设计域、边界条件和载荷条件

图5. 优化结果

该工作主要由华北电力大学新能源电力系统国家重点实验室龙凯课题组完成，龙凯副教授为第一作者兼通讯作者，硕士研究生陈卓为第二作者。该课题受到国家自然科学基金和华能技术基金的资助。

龙凯课题组在瞬态动力学下的二阶缩减算法与拓扑优化列式研究取得重要进展

大型风电机组的叶片展向长弦向短，柔性大，加之工作在随机风速的不确定载荷条件下，易发生弯曲和变形，因而，对叶片动力学特性的研究极其必要。同时风电机组是一个庞大而复杂的多自由度系统，对其进行有限元分析需要耗费极高的计算成本，因而考虑找到一种精度合适、计算效率高的缩减算法用于风电机组的设计中，降低设计成本。

从这一角度出发，提出了一种考虑最大动力响应约束的瞬态振动连续体拓扑优化方法。为解决时域最大响应约束问题，提出了一种积分函数形式的聚合指标。提出了密度滤波与阈值投影相结合的SIMP方法。提出的指标对设计变量的敏感性进行了研究。为了降低计算成本，在瞬态分析中采用了二阶Arnoldi缩减方法(SOAR)。通过典型算例讨论了SOAR方案的聚合参数、加载周期持续时间、间隔时间和基向量个数对最终设计的影响，并实现了明确的配置。通过与最终设计对应的静态响应进行比较，优化结果清楚地表明，结构拓扑优化中瞬态效应是不可忽略的。

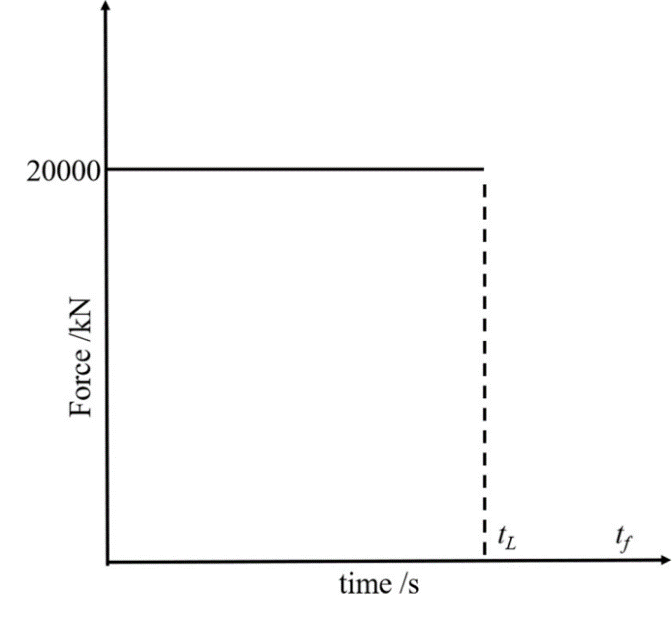
图6．矩形载荷

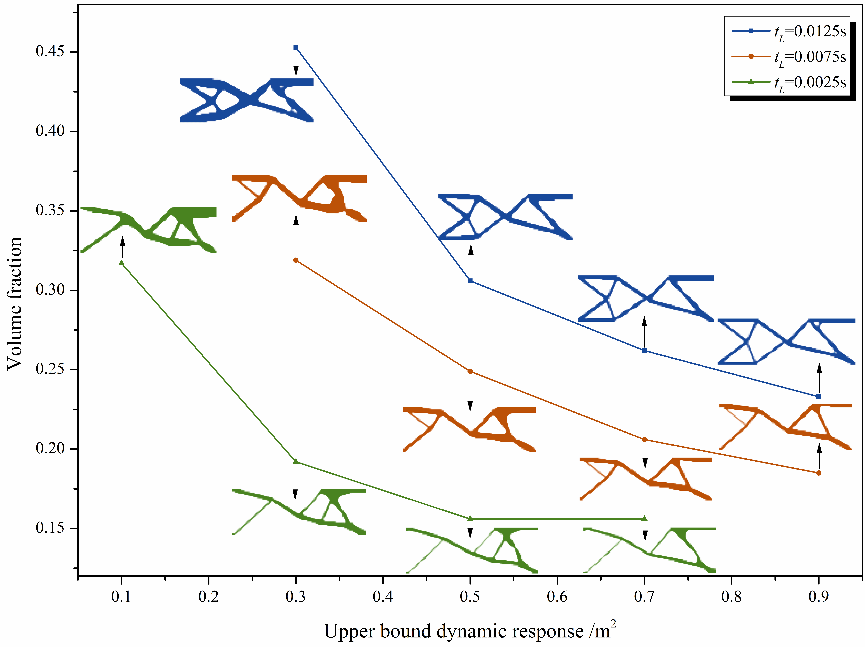
图7.不同最大动力响应下体积比的变化及对应的优化结构

由图7来看，给定的位移越小，材料的体积比就越大，这非常符合工程直觉；同时，加载时间对优化结果有很大的影响，加载时间越长意味着需要越多的材料来保证结构刚度；作为对比，当一个大小为2×104kN的静态载荷施加在最终的结构上时，其位移响应分别为0.170 m2, 0.371 m2, 0.520 m2 and 0.690 m2，当tL取0.0125s时，结构的静刚度超过了动态载荷下的结果，这说明连续体结构的拓扑优化不能忽略惯性和阻尼的影响。

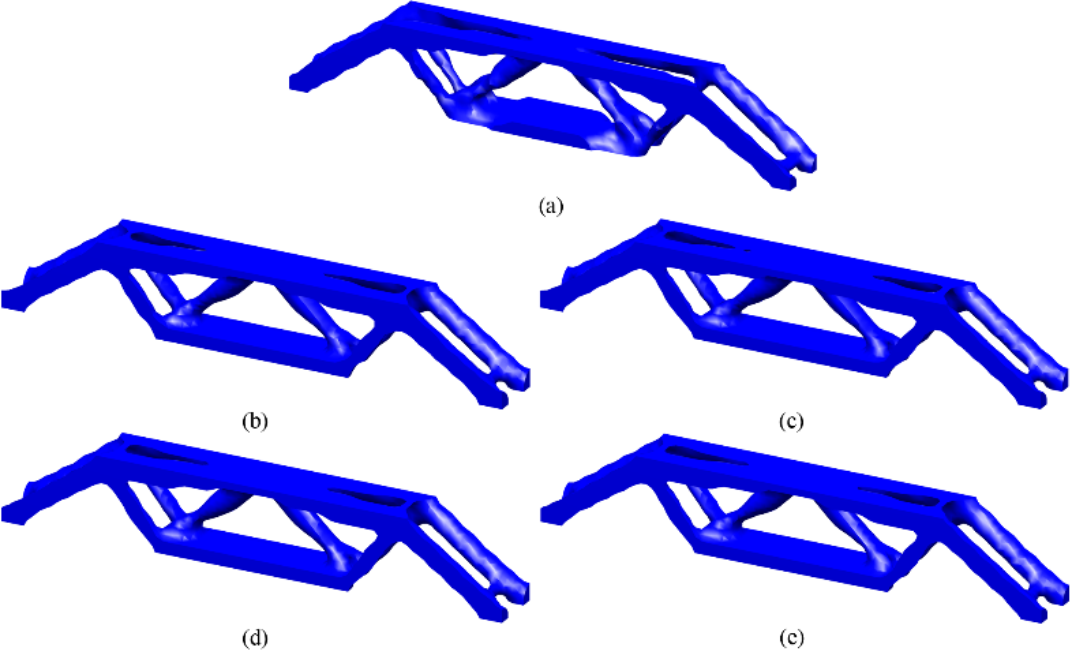
8.不同缩减基个数时的优化结果

表1不同情况下的优化结果

正如预期的那样，通过全分析和SOAR算法得到的最终设计具有相似的结果。通过与表1中的全分析进行比较，可以看出SOAR方法解决的时间显著减少。数值计算结果清楚地证明了该方法对大尺度三维结构处理的有效性。这表明，将SOAR方法用于风电机组的有限元计算中是可行的。

2021年3月1日，该研究成果以“Topology optimization of transient problem with maximum dynamic response constraint using SOAR scheme”为题发表在国际化学领域权威期刊《Frontiers of Mechanical Engineering》上。龙凯副教授为本文的第一作者兼通讯作者，硕士研究生杨晓宇为第二作者，华北电力大学新能源电力系统国家重点实验室是论文唯一通讯单位。

该研究工作得到了国家自然科学基金等项目的资助，论文的发表得到了武汉理工大学文聘副教授，合肥工业大学王选老师的支持。

龙凯课题组在不同泊松比基材料混合的复合材料拓扑优化设计取得重要进展

2020年12月21日，国际著名期刊《Computer Modeling inEngineering & Sciences》在线发表了华北电力大学新能源电力系统国家重点实验室龙凯课题组的最新研究成果“Topological Design of Microstructures of Materials Containing Multiple Phases of Distinct Poisson’s Ratios”，提出了一种计算由两个不同泊松比的各向同性相组成的弹性复合材料最大体模量或剪切模量的方法。

复合材料广泛存在于风电机组的各种零部件中，但目前对复合材料的使用和考量都是基于经验和工程试验，缺乏理论支撑，且经验设计非常不利于机组的安全、工程试验需要耗费大量的人力物力和财力，成本很高。从这一工程实际背景出发，理论研究和计算不同材料之间存在的相互作用对于提高叶片寿命和机组的运行稳定性具有重要意义。从这一背景出发，提出了一种拓扑优化算法，该算法能够求出非常接近理论上界的极值微结构。设计的复合材料的有效力学性能由数值均匀化技术确定。利用不同参数同时插值杨氏模量和泊松比，得到了对设计变量的灵敏度。利用惩罚法建立了固体各向同性材料的优化配方。以最大体积模量或剪切模量为目标函数，以组成相体积分数为约束。采用移动渐近线的方法对设计变量进行更新。通过几个三维数值算例验证了所提出的结构优化方法的有效性。研究了结构设计中泊松比、组成相体积分数等关键参数的影响。从该方法中获得了一系列新的微结构。结果表明，所研究的复合材料的优化体积和剪切模量都非常接近Hashin-Shtrikman-Walpole边界。

表2.计算得到的剪切模量、HSW的剪切模量上限以及相对差值

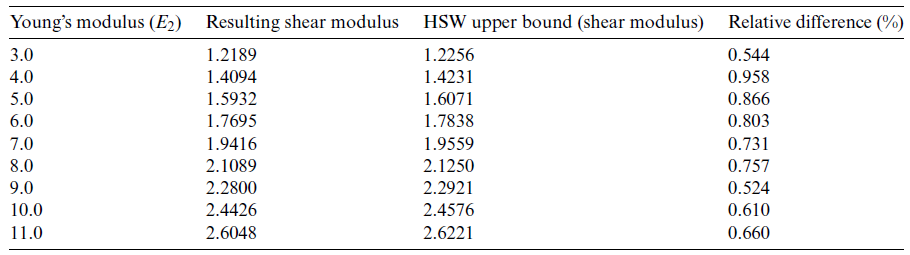
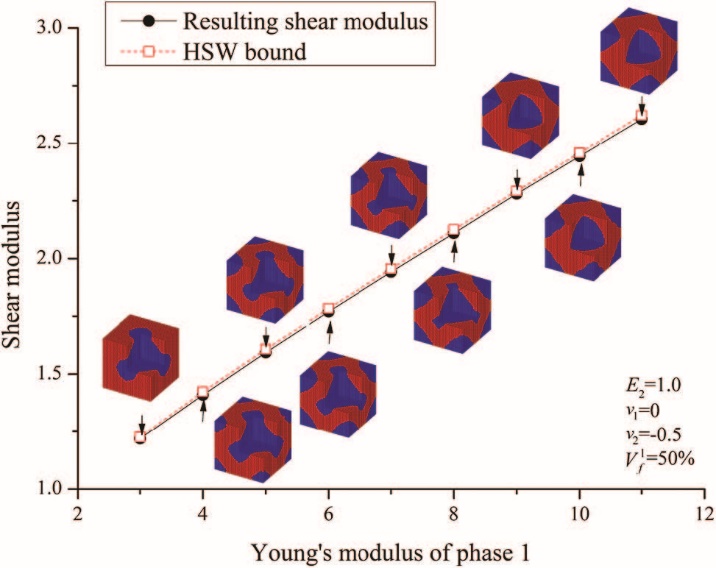
图9. 各种杨氏模量的剪切模量最大化

对不同体积分数的组成相对初始设计进行了研究。第1阶段规定的体积分数为15% ~ 85%。表2列出了得到的剪切模量、HSW剪切模量上限以及它们的相对百分比差异。相应的微观结构拓扑如图9所示。

由表2可知，得到的剪切模量与HSW剪切模量上限的相对百分比差均在3.095%以内。结果表明，在不同的体积分数条件下，可以得到理论上界。从图i可以看出，随着Vf1的增大，各相的拓扑结构发生变化，呈现出不同的形状。该算例证明了该方法在风电中具有潜在的应用价值。

该工作主要由华北电力大学新能源电力系统国家重点实验室龙凯课题组完成，龙凯副教授为第一作者兼通讯作者，硕士研究生杨晓宇为第二作者。该课题受到国家自然科学基金的资助。